
1. 熵(Entropy)
1.1 混乱程度,不确定性,还是信息量?
不同的人对熵有不同的解释:混乱程度,不确定性,惊奇程度,不可预测性,信息量等等,面对如此多的解释,第一次接触时难免困惑。本文第一部分,让我们先一起搞明白 熵 究竟是什么?
信息论中熵的概念首次被香农提出,目的是寻找一种高效/无损地编码信息的方法:以编码后数据的平均长度来衡量高效性,平均长度越小越高效;同时还需满足“无损”的条件,即编码后不能有原始信息的丢失。这样,香农提出了熵的定义:无损编码事件信息的最小平均编码长度。
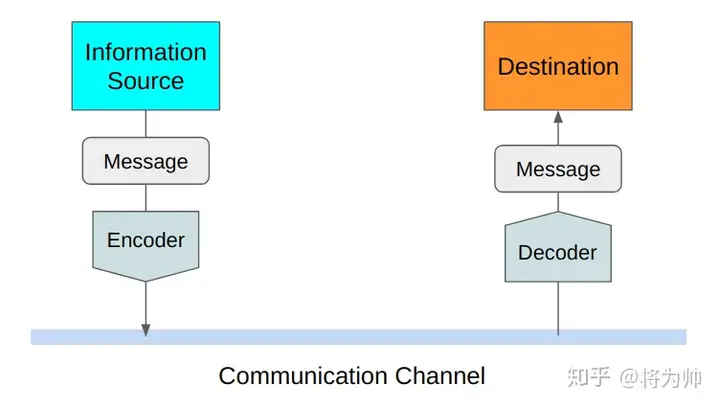
1.2 计算编码长度
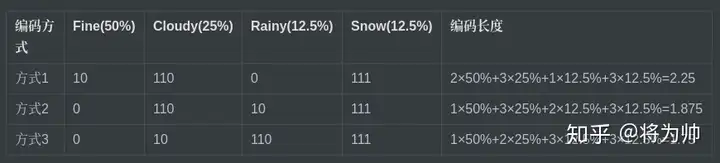
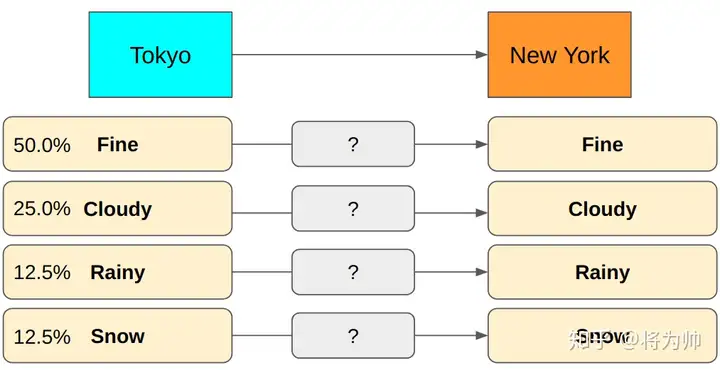
上文提到了熵的定义:无损编码事件信息的最小平均编码长度。编码长度容易理解,但何来的最小,又何来的平均呢?下面以一个例子来说明:假设我们采用二进制编码东京的天气信息,并传输至纽约,其中东京的天气状态有4种可能,对应的概率如下图,每个可能性需要1个编码,东京的天气共需要4个编码。让我们采用3种编码方式,并对比下编码长度。不难发现,方式3编码长度最小,且是平均意义上的最小。方式3胜出的原因在于:对高可能性事件(Fine,Cloudy)用短编码,对低可能性事件(Rainy,Snow)用长编码。表中的3种方式,像是尝试的过程,那么能否直接计算出服从某一概率分布的事件的最小平均编码长度呢?还句话说,能不能直接计算熵?
1.3 直接计算熵
假设一个信息事件有8种可能的状态,且各状态等可能性,即可能性都是12.5%=1/8。我们需要多少位来编码8个值呢?1位可以编码2个值(0或1),2位可以编码2×2=4个值(00,01,10,11),则8个值需要3位,2×2×2=8(000,001,010,011,100,101,110,111)。

我们不能减少任何1位,因为那样会造成歧义,同样我们也不要多于3位来编码8个可能的值。归纳来看,对于具有N种等可能性状态的信息,每种状态的可能性P = 1/N,编码该信息所需的最小编码长度为:
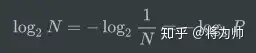
那么计算平均最小长度,也就是熵的公式为:
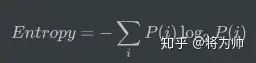
其中P(i)是第i个信息状态的可能性。
回头看看上述编码东京天气的例子,熵 = 1 * 50% + 2 * 25% + 3 * 12.5% + 3 * 12.5% = 1.75

1.4 熵的直观解释
那么熵的那些描述和解释(混乱程度,不确定性,惊奇程度,不可预测性,信息量等)代表了什么呢?
如果熵比较大(即平均编码长度较长),意味着这一信息有较多的可能状态,相应的每个状态的可能性比较低;因此每当来了一个新的信息,我们很难对其作出准确预测,即有着比较大的混乱程度/不确定性/不可预测性。
并且当一个罕见的信息到达时,比一个常见的信息有着更多的信息量,因为它排除了别的很多的可能性,告诉了我们一个确切的信息。在天气的例子中,Rainy发生的概率为12.5%,当接收到该信息时,我们减少了87.5%的不确定性(Fine,Cloudy,Snow);如果接收到Fine(50%)的消息,我们只减少了50%的不确定性。
2. 交叉熵(Cross-Entropy)
2.1 交叉熵损失函数?二分类交叉熵?
熟悉机器学习的人都知道分类模型中会使用交叉熵作损失函数,也一定对吴恩达的机器学习视频中猫分类器使用的二分类交叉熵印象深刻,但交叉熵究竟是什么?本文的第二部分,让我们一起搞明白交叉熵。字面上看,交叉熵分两部分“交叉”和“熵”,首先回顾下熵的公式吧。
2.2 熵的公式
上文中已知一个离散变量 i 的概率分布P(i),熵的公式可以表示为:
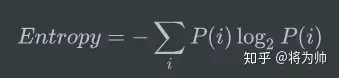
同理,对于连续变量 x 的概率分布P(x),熵的公式可以表示为:
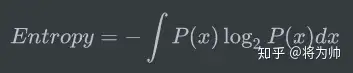
在熵的公式中,对于离散变量和连续变量,我们都是计算了 负的可能性的对数 的期望,代表了该事件理论上的平均最小编码长度,所以熵的公式也可表示如下,公式中的x~P代表我们使用概率分布P来计算期望,熵又可以简写为H:
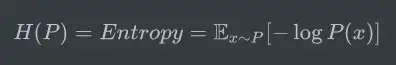
重要的事情再说一遍:“熵是服从某一特定概率分布事件的理论最小平均编码长度”,只要我们知道了任何事件的概率分布,我们就可以计算它的熵;那如果我们不知道事件的概率分布,又想计算熵,该怎么做呢?那我们来对熵做一个估计吧,熵的估计的过程自然而然的引出了交叉熵。
2.3 熵的估计
假如我们现在需要预报东京天气,在真实天气发生之前,我们不可能知道天气的概率分布;但为了下文的讨论,我们需要假设:对东京天气做一段时间的观测后,可以得到真实的概率分布P。
在观测之前,我们只有预估的概率分布Q,使用估计得到的概率分布,可以计算估计的熵:
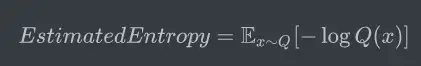
如果Q是真实的概率分布,根据上述公式,我们已经得到了编码东京天气信息的最小平均长度;然而估计的概率分布为我们的公式引入了两部分的不确定性:
- 计算期望的概率分布是Q,与真实的概率分布P不同。
- 计算最小编码长度的概率是 -logQ,与真实的最小编码长度 -logP 不同。
因为估计的概率分布Q影响了上述两个部分(期望和编码长度),所以得到的结果很可能错得离谱,也因此该结果和真实熵的对比无意义。和香农的目标一样,我们希望编码长度尽可能的短,所以我们需要对比我们的编码长度和理论上的最小编码长度(熵)。假设经过观测后,我们得到了真实概率分布P,在天气预报时,就可以使用P计算平均编码长度,实际编码长度基于Q计算,这个计算结果就是P和Q的交叉熵。这样,实际编码长度和理论最小编码长度就有了对比的意义。
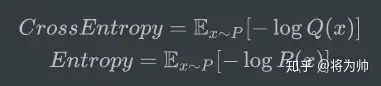
2.4 交叉熵 >= 熵
交叉熵使用H(P,Q)表示,意味着使用P计算期望,使用Q计算编码长度;所以H(P,Q)并不一定等于H(Q,P),除了在P=Q的情况下,H(P,Q) = H(Q,P) = H(P)。
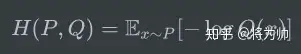
有一点很微妙但很重要:对于期望,我们使用真实概率分布P来计算;对于编码长度,我们使用假设的概率分布Q来计算,因为它是预估用于编码信息的。因为熵是理论上的平均最小编码长度,所以交叉熵只可能大于等于熵。换句话说,如果我们的估计是完美的,即Q=P,那么有H(P,Q) = H(P),否则,H(P,Q) > H(P)。
至此,交叉熵和熵的关系应该比较明确了,下面让我们看看为什么要使用交叉熵作分类损失函数。
2.5 交叉熵作为损失函数
假设一个动物照片的数据集中有5种动物,且每张照片中只有一只动物,每张照片的标签都是one-hot编码。

第一张照片是狗的概率为100%,是其他的动物的概率是0;第二张照片是狐狸的概率是100%,是其他动物的概率是0,其余照片同理;因此可以计算下,每张照片的熵都为0。换句话说,以one-hot编码作为标签的每张照片都有100%的确定度,不像别的描述概率的方式:狗的概率为90%,猫的概率为10%。
假设有两个机器学习模型对第一张照片分别作出了预测:Q1和Q2,而第一张照片的真实标签为[1,0,0,0,0]。

两个模型预测效果如何呢,可以分别计算下交叉熵:
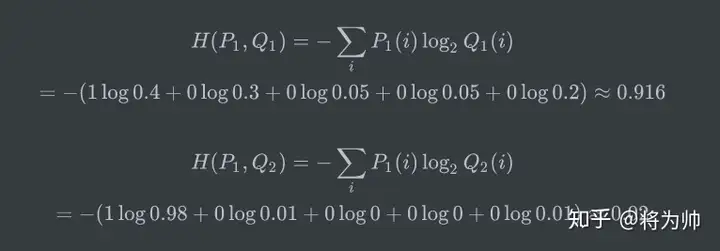
交叉熵对比了模型的预测结果和数据的真实标签,随着预测越来越准确,交叉熵的值越来越小,如果预测完全正确,交叉熵的值就为0。因此,训练分类模型时,可以使用交叉熵作为损失函数。
2.6 二分类交叉熵
在二分类模型中,标签只有是和否两种;这时,可以使用二分类交叉熵作为损失函数。假设数据集中只有猫和狗的照片,则交叉熵公式中只包含两种可能性:
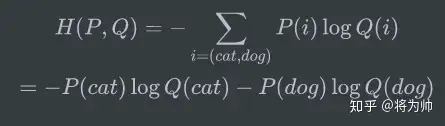
又因为:

所以交叉熵可以表示为:

使用如下定义:
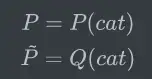
二分类的交叉熵可以写作如下形式,看起来就熟悉多了。

“一文搞懂”系列的初衷有两个:一是记录/分享自己工作学习中的收获,二是奢望 帮助入门者对相关概念有更清晰的认识。“一文搞懂”难免夸大其词,欢迎对文中观点进行讨论/指正/点赞!
- 本文标题:什么是交叉熵损失函数
- 创建时间:2023-06-16 11:00:00
- 本文链接:2023/06/16/深度学习/什么是CrossEntropy,交叉熵/
- 版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!